SEVGİLİ EDEBİYAT DEFTERİ
ŞAİR YAZAR VE OKURLARI,

SONSUZ SEVGİLERİMLE
TÜM İNSANLIK İÇİN YÜREĞİMİ SİZLERE ADADIM BU GÜN.
KURBAN BAYRAMINIZ KUTLU OLSUN.


ŞİİRLERLE TÜRKÜLERLE HALAY ÇEKEREK,
ZEYBEKLER OYNAYIP,HORONLAR TEPEREK
NİCE MUTLU BAYRAMLAR HEPİMİZİN OLSUN.

NE MUTLU TÜRKÜM DİYENE....
.........................................................................................................
SAYGIDEĞER HOCAM SABİHA KÜÇÜKTÜFEKÇİ TARAFINDAN ’’SEVGİLİLER GÜNÜ ’’ ADLI ŞİİRİME YAPILAN YORUM RESMİN AÇIKLAMASI İÇİN GEREKLİ.
Kendisine bana gönderdiği resim ve bilgiler için gönül dolusu teşekkürlerimi ve saygılarımı sunarım hepinizin huzurunda...


Sonsuzda bir olasılık;
en büyük şans dünyaya gelebilmek
insan ömrü kısacık,
şansını iyi kullanmalı
sevgisinin derecesi karnesinde yüreğinin
harareti yüksek,
sevgisi hep pekiyi olmalı
üstüne bir de yıldız ;
insanı sevmek
tanrıyı sevmek kadar kutsal
inan gerisi boş,
hayâl rüyâ, hepsi düş, hepsi masal...



Sonsuza akıp giden bir yıldızsın sen
bir baş iki ayak iki elinle
mutlak bedenden yere düşen
bir gölgesin belki de
dene istersen,
yıldız çizerken
kesintisiz,
ayıramazsın elini yerden;
en tepende en baş
binlerce düş
beyninde yanıp yanıp sönerken
saniyede kaç yıldız doğar
kaçı ölür gökyüzünde hep birden...



Sana sevgiyi,
yaşamayı bahşeden tanrı
çok büyük,
çok çok büyük
ömür boyu düşünsen
hayâl bile edemiyeceğinden...



O HALDE NASIL HESAP VERECEK
BİR İNSANI TEAMMÜDEN ÖLDÜREN?!
(Şaban AKTAŞ)

:::::::::::::
süper bir şiir her yönüyle ...harikasınız hocam..günlerin şiiri ...gökkuşağından kurdeleler bırakıyorum...
sevgim saygım her daim...

bende bilimsel katkıda bulunmak isterim yaradanın en yüce varlık insanı ve insana armağan ettiklerini nasıl mükemmel ölçülerle yarattığını anlamamıza...


:::::::::::::::

ALTIN ORAN

Altın oran, Fi (phi) sayısı olarak bilinir. neticede matematiksel bir kavramdır ve değeri de 1,618 dir. Fibonacci sayıları ve altın oran matematiğin en ilgi çekici konuları arasındadır. Leonardo Fibonacci 13. yüzyılda yaşamış bir Italyan matematikçisiydi.

FIBONACCI DIZISI: 1,1,2,3,5,8,13,21,34,55,89,144....


Bu diziye baktığımız zaman onun basit bir kurala dayanarak oluşturulduğunu görebiliriz. Bu kuralı sözcüklerle ifade edersek; her sayı (ilk ikisi dışında) kendisinden önce gelen iki sayının toplamından oluşmuştur.


Arı kovanlarında yaşayan dişi arıların sayısının erkek arıların sayısına bolundugunde hep aynı sayı elde edilir. Yani 1.618


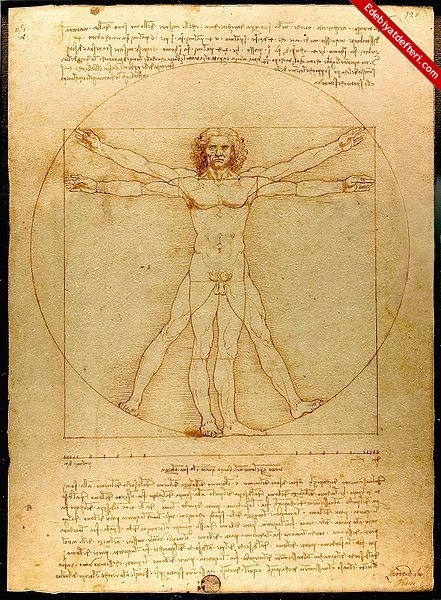
Leonardo Da Vinci nin ünlü cıplak erkegini gosteren Vitruvius adamında da aynı oranlar mevcuttur.


Altın Oran ın Görüldüğü ve Kullanıldığı Yerler


1. Ayçiçeği: Ayçiçeği nin merkezinden dışarıya doğru sağdan sola ve soldan sağa doğru tane sayılarının birbrine oranı, altın oranı verir.


2. Papatya Çiçeği: Papatya Çiçeğinde de ayçiçeğinde olduğu gibi bir altın oran mevcuttur.


3. Insan Kafası: Bildiğiniz gibi her insanın kafasında bir ya da birden fazla saçların çıktığı düğüm noktası denilen bir nokta vardır. Işte bu noktadan çıkan saçlar doğrusal yani dik değil, bir spiral, bir eğri yaparak çıkmaktadır. Işte bu spiralin ya da eğrinin tanjantı yani eğrilik açısı


bize altın oranı verecektir.


4. Insan Vücudu: Insan Vücudunda Altın Oran ın nerelerde görüldüğüne bakalım:


4.1. Kollar: Insan vücudunun bir parçası olan kolları dirsek iki bölüme ayırır(Büyük(üst) bölüm ve küçük(alt) bölüm olarak). Kolumuzun üst bölümünün alt bölüme oranı altın oranı verceği gibi, kolumuzun tamamının üst bölüme oranı yine altın oranı verir.


4.2. Parmaklar: Ellerimizdeki parmaklarla altın oranın ne alakası var diyebilirsiniz. Işte size alaka... Parmaklarınızın üst boğumunun alt boğuma oranı altın oranı vereceği gibi, parmağınızın tamamının üst boğuma oranı yine altın oranı verir.


5. Tavşan: Insan kafasında olduğu gibi tavşanda da aynı özellik vardır.


6. Mısır Piramitleri: Her bir piramitin tabanının yüksekliğine oranı yine altın oranı veriyor.


7. Leonardo da Vinci: Bilindiği gibi Leonardo da Vinci Rönesans devri ünlü ressamlarındandır. Şimdi bu ünlü ressamın çizmiş olduğu tabloları inceleyelim.


7.1. Mona Lisa: Bu tablonun boyunun enine oranı altın oranı verir.


7.2. Aziz Jerome: Yine tablonun boyunun enine oranı bize altın oranı verir.


8. Picasso: Picasso da Leonardo da Vinci gibi ünlü bir ressamdır. Ve resimlerinde bu oranı kullanmıştır.


9. Çam Kozalağı: Çam kozalağındaki taneler kozalağın altındaki sabit bir noktadan kozalağın tepesindeki başka bir sabit noktaya doğru spiraller (eğriler) oluşturarak çıkarlar. Işte bu eğrinin eğrilik açısı altın orandır.


10. Deniz Kabuğu: Denize çoğumuz gitmişizdir. Deniz kabuklarına dikkat edenimiz, belki de kolleksiyon yapanımız vardır. Işte deniz kabuğunun yapısı incelendiğinde bir eğrilik tespit edilmiş ve bu eğriliğin tanjantının altın oran olduğu görülmüştür.


11. Tütün Bitkisi: Tütün Bitkisinin yapraklarının dizilişinde bir eğrilik söz konusudur. Bu eğriliğin tanjantı altın orandır.


12. Eğrelti Otu: Tütün Bitkisindeki aynı özellik Eğrelti Otu nda da vardır.


13. Elektrik Devresi: Altın Oran sadece Matematik ve kainatta değil,


Fizik te de kullanılıyor. Verilen n tane dirençten maximum verim elde etmek için bir paralel bağlama yapılması gerekir. Bu durumda Eşdeğer Direnç, yani Reş= yani altın oran olur.


14. Salyangoz: Salyangozun Kabuğu bir düzleme aktarılırsa, bu düzlem bir dikdörtgen oluşturur (-ki biz bu dikdörtgene altın dikdörtgen diyoruz.-) Işte bu dikdörtgenin boyunun enine oranı yine altın oranı verir.


15. MIMAR SINAN: Mimar Sinan ın da bir çok eserinde bu altın oran görülmektedir. Mesela Süleymaniye ve Selimiye Camileri nin minarelerinde bu oran görülmektedir.


INSAN VÜCUDUNDA ALTIN ORAN


Insan gözünün ALTIN ORAN a bu kadar yakın olmasının, estetik açıdan sürekli olarak ALTIN ORAN a uygun şekil ve yapıları tercih etmesinin bir nedenini, yaşadığı çevre olan doğada hemen her an ALTIN ORAN la karşı karşıya olmasının yanı sıra, kendi vücudunun hemen her noktasında ALTIN ORAN a sahip olmasında arayabiliriz. Aşağıda oranlarda insanında ne kadar ALTIN ORAN örneği olduğunu göreceksiniz:


Boy/ (bölü)Bacak boyu


Beden boyu/kolaltı beden boyu


Tam kol boyu(Boyun-Parmak ucu)/Dirsek - Boğaz


Parmak ucu - omuz/Parmak ucu - Dirsek


Göbek - Omuz/Göbek - Bel


INSAN YÜZÜNDE ALTIN ORAN


Ideal ölçülere sahip bir insan yüzünde de sayısız ALTIN ORAN örnekleri görmek mümkündür:


Yüz yüksekliği/Yüz genişliği


Tepe - Göz yüksekliği/Saç Dibi - Göz Yüksekliği


Göz - çene arası/Burun - çene arası


Alın genişliği/Burun boynu


Göz - Ağız/Burun boyu


Burun altı - çene/Ağız - Çene


Yüz genişliği/Gözbebekleri arası


Gözbebekleri arası/Ağız genişliği


Ağız genişliği/Burun Genişliği


Görüldüğü gibi ALTIN ORAN doğanın güzellik ölçüsü durumundadır. Bu yazıyı okuduktan sonra elinize cetveli alıp eninizi boyunuzu ölçmeye kalkmayın.


ALTIN ORAN a uysada uymasa da insanoğlu ve içinde yaşadığı doğa güzeldir. Yeter ki o güzellikleri görelim...


www.hekimce.com/index.php?kiid=2626



Bu yoruma 1 cevap yazılmış.

Şaban Aktaş | Mesaj gönder | Arkadaş listeme ekle | Engelle | 30.11.2008 15:18:15
Can hocam bilimsel açıklama getirdiğiniz yoruma, insanın bir yıdızı andıran özelliği nereden gelmekte diye açıklama getirmek istersek,iki elini yana açan insan ayaklarını da yana açarsa, el ayak uçlarından ve tepe noktasından geçen noktalar bir dairesel düzlemin üstünde yer alır ve bu dairenin merkezi doğmadan önce anne rahmine bağlı olduğumuz göbeğimizdir.Ve belirttiğim diğer noktalardan çizilecek doğrular kesişince bir yıdız biçimi ortaya çıkmaktadır.En derin saygılarımla gönül zenginliklerinizin, bilimin ufkunda engin keşiflere ulaşması dileğiyle esenlikler sizin olsun....Beni çok mutlu ettiniz...