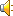MANDELBROT SET

• 11 Eylül 2017 Pazartesi 23:15:34

Mandelbrot kümesi bir kendine benzer kümedir.Herhangi bir milimetrik kâğıtta bir kompleks sayının gerçek kısmı yatay eksende sanal kısmı ise dikey eksende gösterilir.Birkomplaeks sayıyı karesi ile eşleyen bir dönüşüm düşünelim bu dönüşüm için elde ettiğimiz yeni noktaları da milimetrik kâğıtta gösterelim.;Mesela kompleks sayımız 1 olsun karesi 1 olacağından her denemede kağıtta sadece yatay eksende 1 sayısının üstüne nokta koymuş oluruz,benzer şekilde sayıyı 1/2 seçersek ilk iterasyonda eşleneceği sayı 1/4 olacaktır sonra,1/16,1/256,...şeklinde devam ederiz veher iterasyonda sıfıra yaklaşırız,şimdp iye kadar seçtiğimiz kompleks sayıların sanal kısımları hep sıfırdı eger sanal kısmı sıfırrdan farklı seçersek ne olur?Mesela kompleks sayımızı (1,1)olarak seçelim.Bu durumda sayımız 1+i olur.İlk iterasyonda eşleyeceğimiz sayı seçtiğimiz sayının karesi olacağından yeni kompleks sayımız 1+i.i+2i olup i.i=-1 olduğunu bildiğimiz için cevap 2i olacaktır.Böylece (1,1) nokatsını (0,2)noktasına eşlemiş olduk bu ilk iterasyonda elde ettiğimiz bir sonuçtur.İkinci iterasyonda 2i kompleks sayısının karesi -4 olacaktır, milimetrik kâğıtta (-4,0)noktasının işaretleriz.Üçüncü iterasyonda elde edeceğimiz yeni kompleks sayı 16 olacaktır yuani yatay eksende 16 sayısının üstüne nokta koyarız.Şimdiye kadar yaptığımız dönüşümlerde hep bir kompleks sayıyı karesi ile eşledik peki bu sefer farklı bir transform uygulayalım,bir sayıyı alıp karesi ile eşledikten sonra sabit bir sayıyı da sonuca ekleyelim mesela her dönüşümün sonucuna (1,1) =1+i kompleks sayısını ekleyelim.Sayımız 1 olsun karesi gene 1 sabiti ekleresek 2+i yani (2,1) notası na ulaştık,(1,0) noktasını (2,1) noktasına eşledik.Şimdi aynı transformasyonu (2,1)noktasına uygulayalım,ilk olarak bu sayının karesini almalıyız,2+i sayısının karesi 4+4i-1=3+4i bulunur böylece yeni noktamız ,(3,4) noktası bu iteraASSYONU sabit sayımız (1,1) iken 100 defa bilgisayarımızda uyguladığımızı düşünelim, sonra başka bir sabit sayı seçerek mesela 2+2i seçildikten sonra sabit kalan bir s sayı olsun her iterasyondan sonra sonuca 2+2i ekleyelim ve bu işlemi 100 kere tekrearlayalım bulduğumuz sonuçları milimetrik kağıtta işartetleyelim işaretlediğimiz noktaların meydana getirdiği şekilin herhangi birt bölgesine zum yaptığımızda ne kadar zumlarsak zumlayalkım elde ettiğimiz yeni şelklin ilk başta elde ettiğimiz buyuk resim olduğunu görürüz,böylece kendine benzer küme elde ettik günümüzde kendine benzer kümelere FRAKTALLAR deniyor ve MANDELBROT kümesi bir fraktaldır.
Size bir fraktal üretici programı yazayım:
#!/usr/bin/env python
# -*- coding: utf-8 -*-

# Copyright (c) 2013, P. Lutus arachnoid.com
# Released under the GPL www.gnu.org/licenses/gpl.html

from numpy import arange

# dimensional parameters for the set

yl = -1.2
yh = 1.2
ys = .05

xl = -2.05
xh = 0.55
xs = 0.03

def mandelbrot(c):
z = 0
for n in range(10):
z = z*z + c
if(abs(z) > 2):
return ’.’
return ’*’

s = ’’
for y in arange(yl,yh,ys):
for x in arange(xl,xh,xs):
s += mandelbrot(complex(x,y))
s += ’ ’

print(s)
bu programı bilgisayarınızda yazıp uygulayın kolaylıklar dilerim ...